Math Problem Sparks Controversy: The Battle of Interpretations

Post Views: 3

In the era of viral debates and trending challenges, one simple math equation has managed to divide the internet into two fiercely loyal camps. The problem, 8 ÷ 2(2 + 2), may appear straightforward at first glance, but its ambiguity has sparked heated discussions across social media platforms and even among professionals. This viral math puzzle is not just about finding the correct answer—it’s a fascinating exploration of how we interpret mathematical conventions.

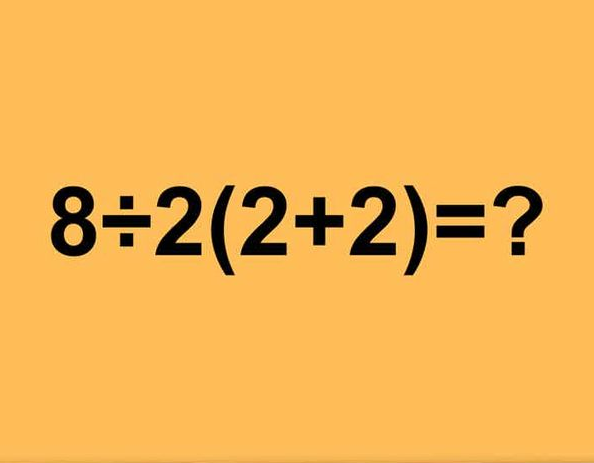
The Viral Equation That Started It All

It all began in 2019 when a seemingly innocent math problem surfaced on Twitter: 8 ÷ 2(2 + 2). The post invited users to solve the equation, but instead of consensus, it unleashed a torrent of disagreement. Two distinct answers—16 and 1—emerged, with each camp passionately defending their calculations.

What made this equation go viral wasn’t just the numbers—it was the polarizing interpretations of the order of operations, a fundamental principle taught in schools worldwide.

Understanding the Order of Operations: PEMDAS Explained

At the heart of the controversy lies PEMDAS, the rule that dictates the sequence in which mathematical operations are performed. PEMDAS stands for:

Parentheses
Exponents
Multiplication
Division
Addition
Subtraction

The rule emphasizes solving operations inside parentheses first, followed by exponents, then multiplication and division from left to right, and finally addition and subtraction from left to right. While it seems simple in theory, the real challenge arises when the equation’s notation creates ambiguity.

The Two Camps: 16 vs. 1

Let’s break down the two interpretations:

The Answer Is 16
- Following PEMDAS, the equation is solved step-by-step:
  1. Solve the parentheses: 2+2=42 + 2 = 42+2=4
  2. Replace the parentheses with the result: 8÷2(4)8 ÷ 2(4)8÷2(4)
  3. Treat the equation as 8÷2×48 ÷ 2 × 48÷2×4, performing division and multiplication from left to right:
    - 8÷2=48 ÷ 2 = 48÷2=4
    - 4×4=164 × 4 = 164×4=16
- According to this method, the answer is clearly 16.
The Answer Is 1
- This interpretation groups the terms differently:
  1. Solve the parentheses: 2+2=42 + 2 = 42+2=4
  2. Treat 2(4)2(4)2(4) as a single term (implied multiplication): 8÷[2(4)]8 ÷ [2(4)]8÷[2(4)]
  3. Simplify: 8÷8=18 ÷ 8 = 18÷8=1
- Using this approach, the answer is 1.

Why the Ambiguity?

The confusion stems from the way the equation is written. In mathematics, implied multiplication (as in 2(4)2(4)2(4)) is often prioritized over division. However, modern conventions treat all multiplication and division operations equally, solving them from left to right.

Mike Breen, from the American Mathematical Society, weighed in on the debate, acknowledging that while 16 is the correct answer by strict PEMDAS rules, the ambiguous notation leaves room for misinterpretation. He explained that the equation could have been written more explicitly to avoid confusion, such as:

(8 ÷ 2)(2 + 2) to make the answer 16 clear.
8 ÷ [2(2 + 2)] to make the answer 1 unambiguous.

Expert Insights on the Equation

To clarify the debate, Rhett Allain, a Physics Professor at Southeastern Louisiana University, emphasized that the problem highlights a gap between mathematical notation and interpretation. He explained that while professionals often work with clear formulas, ambiguities in casual math problems can lead to multiple “correct” answers, depending on conventions.

Allain also pointed out that this problem isn’t just about math—it’s about how we communicate mathematical ideas. For everyday problems, clarity in notation is just as important as accuracy in solving them.

Why This Math Problem Went Viral

So, why did this equation capture the internet’s attention? It’s more than just a tricky puzzle—it taps into deeper themes:

Nostalgia for Math Class: Many people enjoy revisiting high school math concepts like PEMDAS, even if they don’t use them daily.
Friendly Competition: The divide between Team 16 and Team 1 creates a sense of rivalry, encouraging users to prove their answer is correct.
Universal Accessibility: Unlike niche brainteasers, this equation is simple enough for anyone to attempt, making it an inclusive challenge.

This viral sensation underscores the power of math to spark curiosity and discussion, even outside academic settings.

The Broader Lesson: Communication in Mathematics

The debate around 8 ÷ 2(2 + 2) highlights an important lesson: clear communication is crucial in mathematics. While the problem may seem trivial, it reveals how small ambiguities can lead to vastly different interpretations.

In real-world applications, such as engineering or data analysis, unclear equations could result in costly errors. This underscores the need for precise notation and careful consideration when writing mathematical expressions.

The Legacy of the Viral Math Problem

Years after it first surfaced, the debate over this equation continues to pop up in discussions and challenges. Whether you’re on Team 16 or Team 1, this problem serves as a reminder of the beauty and complexity of mathematics. It has inspired people to revisit foundational concepts, question assumptions, and appreciate the intricacies of problem-solving.

More importantly, it demonstrates that math isn’t just about numbers—it’s about interpretation, reasoning, and communication. The next time you encounter a puzzling equation, take a moment to consider not just the answer, but how you arrived at it.

Conclusion: Math as a Gateway to Curiosity

The controversy over 8 ÷ 2(2 + 2) may never fully settle, but that’s part of its charm. This viral math problem has transcended its numerical roots to become a cultural phenomenon, sparking debates, expert analyses, and even friendships (or rivalries) along the way.

Whether you arrived at 16 or 1, the real winner here is the conversation it inspired. Math, after all, isn’t just about solving problems—it’s about engaging with the world in new and thought-provoking ways. So, the next time you see a seemingly simple equation, don’t just solve it. Explore it, question it, and most importantly, enjoy the journey.